Advanced Model Insights¶
This notebook explores additional options for model insights added in the v2.7 release of the DataRobot API.
Prerequisites¶
In order to run this notebook yourself, you will need the following:
- This notebook. If you are viewing this in the HTML documentation bundle, you can download all of the example notebooks and supporting materials from Downloads.
- The dataset required for this notebook. This is in the same directory as this notebook.
- A DataRobot API token. You can find your API token by logging into the DataRobot Web User Interface and looking in your
Profile.
Preparation¶
This notebook explores additional options for model insights added in the v2.7 release of the DataRobot API.
Let’s start with importing some packages that will help us with presentation (if you don’t have them installed already, you’ll have to install them to run this notebook).
[1]:
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.ticker as mtick
import pandas as pd
import datarobot as dr
import numpy as np
from datarobot.enums import AUTOPILOT_MODE
from datarobot.errors import ClientError
Configure the Python Client¶
Configuring the client requires the following two things:
- A DataRobot endpoint - where the API server can be found
- A DataRobot API token - a token the server uses to identify and validate the user making API requests
The endpoint is usually the URL you would use to log into the DataRobot Web User Interface (e.g., https://app.datarobot.com) with “/api/v2/” appended, e.g., (https://app.datarobot.com/api/v2/).
You can find your API token by logging into the DataRobot Web User Interface and looking in your Profile.
The Python client can be configured in several ways. The example we’ll use in this notebook is to point to a yaml file that has the information. This is a text file containing two lines like this:
endpoint: https://app.datarobot.com/api/v2/
token: not-my-real-token
If you want to run this notebook without changes, please save your configuration in a file located under your home directory called ~/.config/datarobot/drconfig.yaml.
[2]:
# Initialization with arguments
# dr.Client(token='<API TOKEN>', endpoint='https://<YOUR ENDPOINT>/api/v2/')
# Initialization with a config file in the same directory as this notebook
# dr.Client(config_path='drconfig.yaml')
# Initialization with a config file located at
# ~/.config/datarobot/dr.config.yaml
dr.Client()
[2]:
<datarobot.rest.RESTClientObject at 0x1119c0d90>
Create Project with features¶
Create a new project using the 10K_diabetes dataset. This dataset contains a binary classification on the target readmitted. This project is an excellent example of the advanced model insights available from DataRobot models.
[3]:
url = 'https://s3.amazonaws.com/datarobot_public_datasets/10k_diabetes.xlsx'
project = dr.Project.create(url, project_name='10K Advanced Modeling')
print('Project ID: {}'.format(project.id))
Project ID: 5c0008e06523cd0233c49fe4
[4]:
# Increase the worker count to your maximum available the project runs faster.
project.set_worker_count(-1)
[4]:
Project(10K Advanced Modeling)
[5]:
target_feature_name = 'readmitted'
project.set_target(target_feature_name, mode=AUTOPILOT_MODE.QUICK)
[5]:
Project(10K Advanced Modeling)
[6]:
project.wait_for_autopilot()
In progress: 14, queued: 0 (waited: 0s)
In progress: 14, queued: 0 (waited: 1s)
In progress: 14, queued: 0 (waited: 1s)
In progress: 14, queued: 0 (waited: 2s)
In progress: 14, queued: 0 (waited: 3s)
In progress: 14, queued: 0 (waited: 5s)
In progress: 11, queued: 0 (waited: 9s)
In progress: 10, queued: 0 (waited: 16s)
In progress: 6, queued: 0 (waited: 29s)
In progress: 1, queued: 0 (waited: 49s)
In progress: 7, queued: 0 (waited: 70s)
In progress: 1, queued: 0 (waited: 90s)
In progress: 16, queued: 0 (waited: 111s)
In progress: 10, queued: 0 (waited: 131s)
In progress: 6, queued: 0 (waited: 151s)
In progress: 2, queued: 0 (waited: 172s)
In progress: 0, queued: 0 (waited: 192s)
In progress: 5, queued: 0 (waited: 213s)
In progress: 1, queued: 0 (waited: 233s)
In progress: 4, queued: 0 (waited: 253s)
In progress: 1, queued: 0 (waited: 274s)
In progress: 1, queued: 0 (waited: 294s)
In progress: 0, queued: 0 (waited: 315s)
In progress: 0, queued: 0 (waited: 335s)
[7]:
models = project.get_models()
model = models[0]
model
[7]:
Model(u'AVG Blender')
Let’s set some color constants to replicate visual style of DataRobot lift chart.
[8]:
dr_dark_blue = '#08233F'
dr_blue = '#1F77B4'
dr_orange = '#FF7F0E'
dr_red = '#BE3C28'
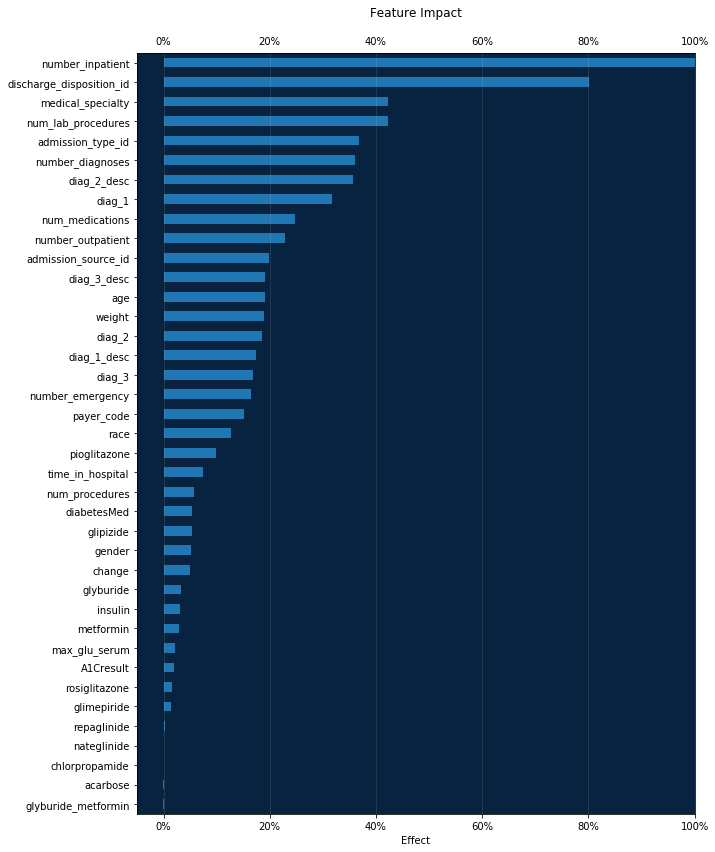
Feature Impact¶
Feature Impact is available for all model types and works by altering input data and observing the effect on a model’s score. It is an on-demand feature, meaning that you must initiate a calculation to see the results. Once you have had DataRobot compute the feature impact for a model, that information is saved with the project.
Feature Impact measures how important a feature is in the context of a model. That is, it measures how much the accuracy of a model would decrease if that feature were removed.
[9]:
feature_impacts = model.get_or_request_feature_impact()
[10]:
# Formats the ticks from a float into a percent
percent_tick_fmt = mtick.PercentFormatter(xmax=1.0)
impact_df = pd.DataFrame(feature_impacts)
impact_df.sort_values(by='impactNormalized', ascending=True, inplace=True)
# Positive values are blue, negative are red
bar_colors = impact_df.impactNormalized.apply(lambda x: dr_red if x < 0
else dr_blue)
ax = impact_df.plot.barh(x='featureName', y='impactNormalized',
legend=False,
color=bar_colors,
figsize=(10, 14))
ax.xaxis.set_major_formatter(percent_tick_fmt)
ax.xaxis.set_tick_params(labeltop=True)
ax.xaxis.grid(True, alpha=0.2)
ax.set_facecolor(dr_dark_blue)
plt.ylabel('')
plt.xlabel('Effect')
plt.xlim((None, 1)) # Allow for negative impact
plt.title('Feature Impact', y=1.04)
[10]:
Text(0.5,1.04,'Feature Impact')
Feature Histogram¶
Feature histogram is a popular EDA tool for visualizing features. Using DataRobot feature histogram API it is easy to draw them.
For starters, let us set up two convenient functions.
First helper function below - matplotlib_pair_histogram - will be used to draw histograms paired with project target feature. We also attach an orange mark to every histogram bin with average target feature value for rows in that bin.
[11]:
def matplotlib_pair_histogram(labels, counts, target_avgs,
bin_count, ax1, feature):
# Rotate categorical labels
if feature.feature_type in ['Categorical', 'Text']:
ax1.tick_params(axis='x', rotation=45)
ax1.set_ylabel(feature.name, color=dr_blue)
ax1.bar(labels, counts, color=dr_blue)
# Instantiate a second axes that shares the same x-axis
ax2 = ax1.twinx()
ax2.set_ylabel(target_feature_name, color=dr_orange)
ax2.plot(labels, target_avgs, marker='o', lw=1, color=dr_orange)
ax1.set_facecolor(dr_dark_blue)
title = 'Histogram for {} ({} bins)'.format(feature.name, bin_count)
ax1.set_title(title)
Let us also create high level function draw_feature_histogram, which will get histogram data and draw histogram using helper function we have just created. But first let try to retrieve downsampled histogram data and have a look at it:
[12]:
feature = dr.Feature.get(project.id, 'num_lab_procedures')
feature.get_histogram(bin_limit=6).plot
[12]:
[{'count': 755, 'label': u'1.0', 'target': 0.36026490066225164},
{'count': 895, 'label': u'14.5', 'target': 0.3240223463687151},
{'count': 1875, 'label': u'28.0', 'target': 0.3744},
{'count': 2159, 'label': u'41.5', 'target': 0.38490041685965726},
{'count': 1603, 'label': u'55.0', 'target': 0.45414847161572053},
{'count': 557, 'label': u'68.5', 'target': 0.5080789946140036}]
For best accuracy it is recommended to use divisors of 60 for bin_limit, but actully any values <= 60 can be used as well.
target values are basically project target input average values for that bins. Please refer to FeatureHistogram for documentation details.
So, our high level function draw_feature_histogram will be like:
[14]:
def draw_feature_histogram(feature_name, bin_count):
feature = dr.Feature.get(project.id, feature_name)
# Retrieve downsampled histogram data from server
# based on desired bin count
data = feature.get_histogram(bin_count).plot
labels = [row['label'] for row in data]
counts = [row['count'] for row in data]
target_averages = [row['target'] for row in data]
f, axarr = plt.subplots()
f.set_size_inches((10, 4))
matplotlib_pair_histogram(labels, counts, target_averages,
bin_count, axarr, feature)
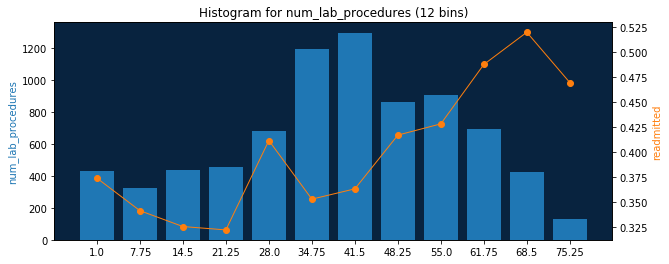
Done! Now we can just specify feature name and desired bin count to get feature histograms. Example for numerical feature:
[15]:
draw_feature_histogram('num_lab_procedures', 12)
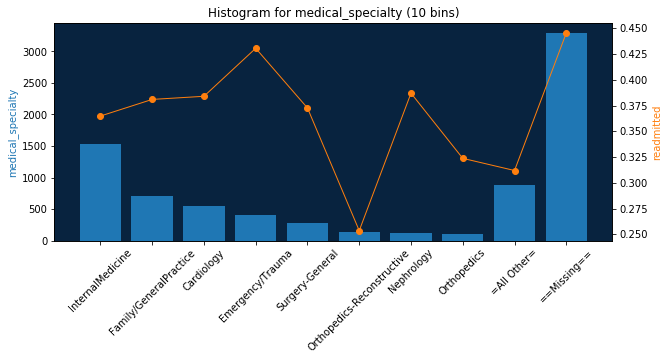
Categorical and other feature types are supported as well:
[16]:
draw_feature_histogram('medical_specialty', 10)
Lift Chart¶
A lift chart will show you how close in general model predictions are to the actual target values in the training data.
The lift chart data we retrieve from the server includes the average model prediction and the average actual target values, sorted by the prediction values in ascending order and split into up to 60 bins.
bin_weight parameter shows how much weight is in each bin (number of rows for unweighted projects).
[17]:
lc = model.get_lift_chart('validation')
lc
[17]:
LiftChart(validation)
[18]:
bins_df = pd.DataFrame(lc.bins)
bins_df.head()
[18]:
| actual | bin_weight | predicted | |
|---|---|---|---|
| 0 | 0.037037 | 27.0 | 0.097886 |
| 1 | 0.037037 | 27.0 | 0.137739 |
| 2 | 0.076923 | 26.0 | 0.162243 |
| 3 | 0.185185 | 27.0 | 0.173459 |
| 4 | 0.333333 | 27.0 | 0.188488 |
Let’s define our rebinning and plotting functions.
[19]:
def rebin_df(raw_df, number_of_bins):
cols = ['bin', 'actual_mean', 'predicted_mean', 'bin_weight']
new_df = pd.DataFrame(columns=cols)
current_prediction_total = 0
current_actual_total = 0
current_row_total = 0
x_index = 1
bin_size = 60 / number_of_bins
for rowId, data in raw_df.iterrows():
current_prediction_total += data['predicted'] * data['bin_weight']
current_actual_total += data['actual'] * data['bin_weight']
current_row_total += data['bin_weight']
if ((rowId + 1) % bin_size == 0):
x_index += 1
bin_properties = {
'bin': ((round(rowId + 1) / 60) * number_of_bins),
'actual_mean': current_actual_total / current_row_total,
'predicted_mean': current_prediction_total / current_row_total,
'bin_weight': current_row_total
}
new_df = new_df.append(bin_properties, ignore_index=True)
current_prediction_total = 0
current_actual_total = 0
current_row_total = 0
return new_df
def matplotlib_lift(bins_df, bin_count, ax):
grouped = rebin_df(bins_df, bin_count)
ax.plot(range(1, len(grouped) + 1), grouped['predicted_mean'],
marker='+', lw=1, color=dr_blue)
ax.plot(range(1, len(grouped) + 1), grouped['actual_mean'],
marker='*', lw=1, color=dr_orange)
ax.set_xlim([0, len(grouped) + 1])
ax.set_facecolor(dr_dark_blue)
ax.legend(loc='best')
ax.set_title('Lift chart {} bins'.format(bin_count))
ax.set_xlabel('Sorted Prediction')
ax.set_ylabel('Value')
return grouped
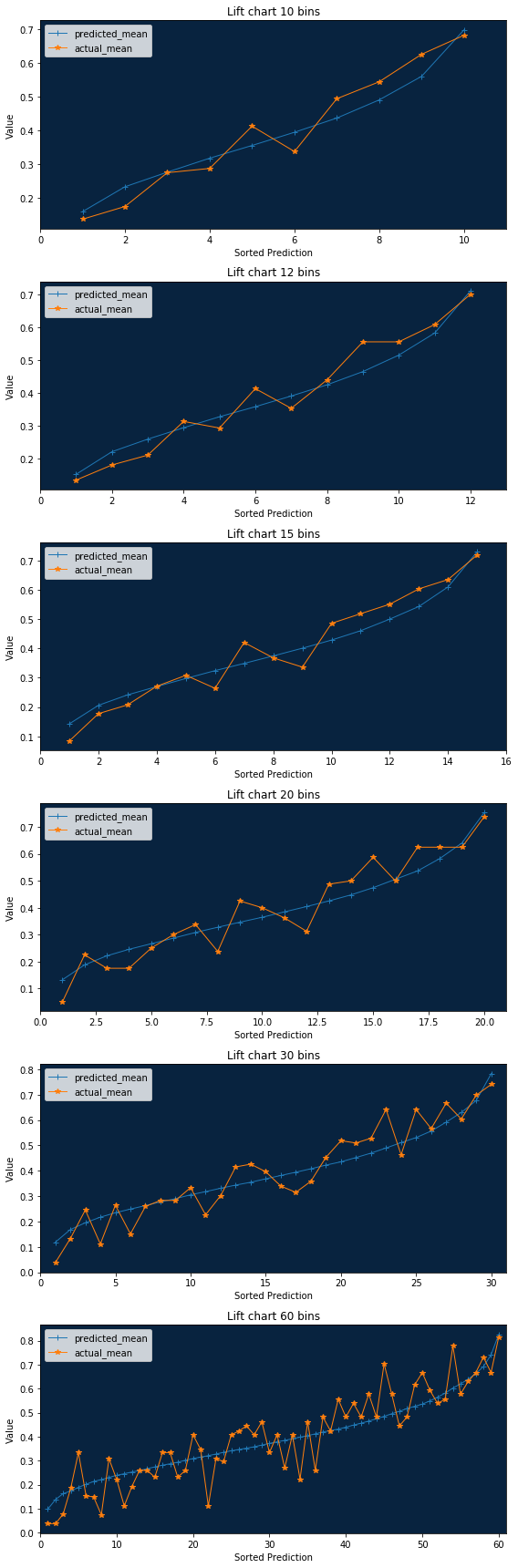
Now we can show all lift charts we propose in DataRobot web application.
Note 1 : While this method will work for any bin count less then 60 - the most reliable result will be achieved when the number of bins is a divisor of 60.
Note 2 : This visualization method will NOT work for bin count > 60 because DataRobot does not provide enough information for a larger resolution.
[20]:
bin_counts = [10, 12, 15, 20, 30, 60]
f, axarr = plt.subplots(len(bin_counts))
f.set_size_inches((8, 4 * len(bin_counts)))
rebinned_dfs = []
for i in range(len(bin_counts)):
rebinned_dfs.append(matplotlib_lift(bins_df, bin_counts[i], axarr[i]))
plt.tight_layout()
Rebinned Data¶
You may want to interact with the raw re-binned data for use in third party tools, or for additional evaluation.
[21]:
for rebinned in rebinned_dfs:
print('Number of bins: {}'.format(len(rebinned.index)))
print(rebinned)
Number of bins: 10
bin actual_mean predicted_mean bin_weight
0 1.0 0.13750 0.159916 160.0
1 2.0 0.17500 0.233332 160.0
2 3.0 0.27500 0.276564 160.0
3 4.0 0.28750 0.317841 160.0
4 5.0 0.41250 0.355449 160.0
5 6.0 0.33750 0.394435 160.0
6 7.0 0.49375 0.436481 160.0
7 8.0 0.54375 0.490176 160.0
8 9.0 0.62500 0.559797 160.0
9 10.0 0.68125 0.697142 160.0
Number of bins: 12
bin actual_mean predicted_mean bin_weight
0 1.0 0.134328 0.151886 134.0
1 2.0 0.180451 0.220872 133.0
2 3.0 0.210526 0.259316 133.0
3 4.0 0.313433 0.294237 134.0
4 5.0 0.293233 0.327699 133.0
5 6.0 0.413534 0.358398 133.0
6 7.0 0.353383 0.390993 133.0
7 8.0 0.440299 0.425269 134.0
8 9.0 0.556391 0.465567 133.0
9 10.0 0.556391 0.515761 133.0
10 11.0 0.609023 0.583067 133.0
11 12.0 0.701493 0.712181 134.0
Number of bins: 15
bin actual_mean predicted_mean bin_weight
0 1.0 0.084112 0.142650 107.0
1 2.0 0.177570 0.206029 107.0
2 3.0 0.207547 0.241613 106.0
3 4.0 0.271028 0.269917 107.0
4 5.0 0.308411 0.297614 107.0
5 6.0 0.264151 0.324330 106.0
6 7.0 0.420561 0.349149 107.0
7 8.0 0.367925 0.374717 106.0
8 9.0 0.336449 0.400959 107.0
9 10.0 0.485981 0.428771 107.0
10 11.0 0.518868 0.460771 106.0
11 12.0 0.551402 0.500419 107.0
12 13.0 0.603774 0.543591 106.0
13 14.0 0.635514 0.610431 107.0
14 15.0 0.719626 0.730594 107.0
Number of bins: 20
bin actual_mean predicted_mean bin_weight
0 1.0 0.0500 0.132253 80.0
1 2.0 0.2250 0.187579 80.0
2 3.0 0.1750 0.221244 80.0
3 4.0 0.1750 0.245419 80.0
4 5.0 0.2500 0.266226 80.0
5 6.0 0.3000 0.286902 80.0
6 7.0 0.3375 0.308215 80.0
7 8.0 0.2375 0.327466 80.0
8 9.0 0.4250 0.346325 80.0
9 10.0 0.4000 0.364573 80.0
10 11.0 0.3625 0.384512 80.0
11 12.0 0.3125 0.404358 80.0
12 13.0 0.4875 0.425218 80.0
13 14.0 0.5000 0.447743 80.0
14 15.0 0.5875 0.474525 80.0
15 16.0 0.5000 0.505826 80.0
16 17.0 0.6250 0.536862 80.0
17 18.0 0.6250 0.582731 80.0
18 19.0 0.6250 0.640753 80.0
19 20.0 0.7375 0.753532 80.0
Number of bins: 30
bin actual_mean predicted_mean bin_weight
0 1.0 0.037037 0.117812 54.0
1 2.0 0.132075 0.167957 53.0
2 3.0 0.245283 0.194772 53.0
3 4.0 0.111111 0.217077 54.0
4 5.0 0.264151 0.234340 53.0
5 6.0 0.150943 0.248885 53.0
6 7.0 0.259259 0.262677 54.0
7 8.0 0.283019 0.277293 53.0
8 9.0 0.283019 0.289984 53.0
9 10.0 0.333333 0.305103 54.0
10 11.0 0.226415 0.317688 53.0
11 12.0 0.301887 0.330972 53.0
12 13.0 0.415094 0.343545 53.0
13 14.0 0.425926 0.354649 54.0
14 15.0 0.396226 0.368169 53.0
15 16.0 0.339623 0.381265 53.0
16 17.0 0.314815 0.394318 54.0
17 18.0 0.358491 0.407725 53.0
18 19.0 0.452830 0.422268 53.0
19 20.0 0.518519 0.435153 54.0
20 21.0 0.509434 0.452046 53.0
21 22.0 0.528302 0.469495 53.0
22 23.0 0.641509 0.489711 53.0
23 24.0 0.462963 0.510929 54.0
24 25.0 0.641509 0.530756 53.0
25 26.0 0.566038 0.556426 53.0
26 27.0 0.666667 0.591609 54.0
27 28.0 0.603774 0.629608 53.0
28 29.0 0.698113 0.676879 53.0
29 30.0 0.740741 0.783314 54.0
Number of bins: 60
bin actual_mean predicted_mean bin_weight
0 1.0 0.037037 0.097886 27.0
1 2.0 0.037037 0.137739 27.0
2 3.0 0.076923 0.162243 26.0
3 4.0 0.185185 0.173459 27.0
4 5.0 0.333333 0.188488 27.0
5 6.0 0.153846 0.201298 26.0
6 7.0 0.148148 0.213213 27.0
7 8.0 0.074074 0.220940 27.0
8 9.0 0.307692 0.229899 26.0
9 10.0 0.222222 0.238617 27.0
10 11.0 0.111111 0.245402 27.0
11 12.0 0.192308 0.252501 26.0
12 13.0 0.259259 0.258865 27.0
13 14.0 0.259259 0.266489 27.0
14 15.0 0.230769 0.273597 26.0
15 16.0 0.333333 0.280852 27.0
16 17.0 0.333333 0.286678 27.0
17 18.0 0.230769 0.293418 26.0
18 19.0 0.259259 0.301547 27.0
19 20.0 0.407407 0.308660 27.0
20 21.0 0.346154 0.314679 26.0
21 22.0 0.111111 0.320585 27.0
22 23.0 0.307692 0.327277 26.0
23 24.0 0.296296 0.334530 27.0
24 25.0 0.407407 0.340926 27.0
25 26.0 0.423077 0.346264 26.0
26 27.0 0.444444 0.351782 27.0
27 28.0 0.407407 0.357515 27.0
28 29.0 0.461538 0.364479 26.0
29 30.0 0.333333 0.371723 27.0
30 31.0 0.407407 0.378530 27.0
31 32.0 0.269231 0.384105 26.0
32 33.0 0.407407 0.390886 27.0
33 34.0 0.222222 0.397751 27.0
34 35.0 0.461538 0.403918 26.0
35 36.0 0.259259 0.411391 27.0
36 37.0 0.481481 0.419135 27.0
37 38.0 0.423077 0.425521 26.0
38 39.0 0.555556 0.431010 27.0
39 40.0 0.481481 0.439296 27.0
40 41.0 0.538462 0.448068 26.0
41 42.0 0.481481 0.455876 27.0
42 43.0 0.576923 0.464854 26.0
43 44.0 0.481481 0.473965 27.0
44 45.0 0.703704 0.484397 27.0
45 46.0 0.576923 0.495230 26.0
46 47.0 0.444444 0.505163 27.0
47 48.0 0.481481 0.516694 27.0
48 49.0 0.615385 0.526190 26.0
49 50.0 0.666667 0.535152 27.0
50 51.0 0.592593 0.548849 27.0
51 52.0 0.538462 0.564293 26.0
52 53.0 0.555556 0.581138 27.0
53 54.0 0.777778 0.602079 27.0
54 55.0 0.576923 0.619633 26.0
55 56.0 0.629630 0.639213 27.0
56 57.0 0.666667 0.662629 27.0
57 58.0 0.730769 0.691678 26.0
58 59.0 0.666667 0.740971 27.0
59 60.0 0.814815 0.825658 27.0
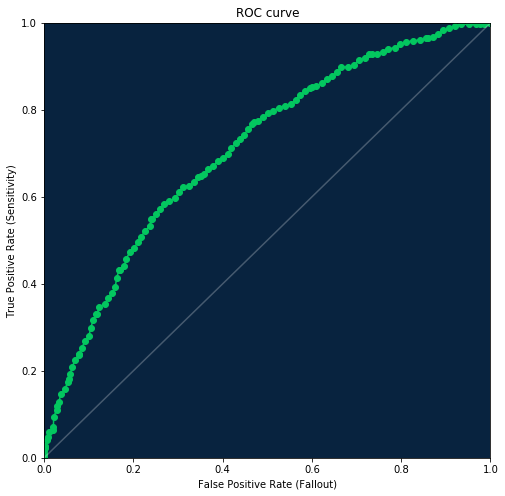
ROC curve¶
The receiver operating characteristic curve, or ROC curve, is a graphical plot that illustrates the performance of a binary classifier system as its discrimination threshold is varied. The curve is created by plotting the true positive rate (TPR) against the false positive rate (FPR) at various threshold settings.
To retrieve ROC curve information use the Model.get_roc_curve method.
[22]:
roc = model.get_roc_curve('validation')
roc
[22]:
RocCurve(validation)
[23]:
df = pd.DataFrame(roc.roc_points)
df.head()
[23]:
| accuracy | f1_score | false_negative_score | false_positive_rate | false_positive_score | matthews_correlation_coefficient | negative_predictive_value | positive_predictive_value | threshold | true_negative_rate | true_negative_score | true_positive_rate | true_positive_score | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.603125 | 0.000000 | 635 | 0.000000 | 0 | 0.000000 | 0.603125 | 0.0000 | 1.000000 | 1.000000 | 965 | 0.000000 | 0 |
| 1 | 0.604375 | 0.006279 | 633 | 0.000000 | 0 | 0.043612 | 0.603880 | 1.0000 | 0.919849 | 1.000000 | 965 | 0.003150 | 2 |
| 2 | 0.606875 | 0.018721 | 629 | 0.000000 | 0 | 0.075632 | 0.605395 | 1.0000 | 0.881041 | 1.000000 | 965 | 0.009449 | 6 |
| 3 | 0.609375 | 0.031008 | 625 | 0.000000 | 0 | 0.097764 | 0.606918 | 1.0000 | 0.839455 | 1.000000 | 965 | 0.015748 | 10 |
| 4 | 0.611875 | 0.046083 | 620 | 0.001036 | 1 | 0.111058 | 0.608586 | 0.9375 | 0.798130 | 0.998964 | 964 | 0.023622 | 15 |
Threshold operations¶
You can get the recommended threshold value with maximal F1 score using RocCurve.get_best_f1_threshold method. That is the same threshold that is preselected in DataRobot when you open “ROC curve” tab.
[24]:
threshold = roc.get_best_f1_threshold()
threshold
[24]:
0.3410205659739286
To estimate metrics for different threshold values just pass it to the RocCurve.estimate_threshold method. This will produce the same results as updating threshold on the DataRobot “ROC curve” tab.
[25]:
metrics = roc.estimate_threshold(threshold)
metrics
[25]:
{'accuracy': 0.62625,
'f1_score': 0.6215189873417721,
'false_negative_score': 144,
'false_positive_rate': 0.47046632124352333,
'false_positive_score': 454,
'matthews_correlation_coefficient': 0.30124189206636187,
'negative_predictive_value': 0.7801526717557252,
'positive_predictive_value': 0.5195767195767196,
'threshold': 0.3410205659739286,
'true_negative_rate': 0.5295336787564767,
'true_negative_score': 511,
'true_positive_rate': 0.7732283464566929,
'true_positive_score': 491}
Confusion matrix¶
Using a few keys from the retrieved metrics we now can build a confusion matrix for the selected threshold.
[26]:
roc_df = pd.DataFrame({
'Predicted Negative': [metrics['true_negative_score'],
metrics['false_negative_score'],
metrics['true_negative_score'] + metrics[
'false_negative_score']],
'Predicted Positive': [metrics['false_positive_score'],
metrics['true_positive_score'],
metrics['true_positive_score'] + metrics[
'false_positive_score']],
'Total': [len(roc.negative_class_predictions),
len(roc.positive_class_predictions),
len(roc.negative_class_predictions) + len(
roc.positive_class_predictions)]})
roc_df.index = pd.MultiIndex.from_tuples([
('Actual', '-'), ('Actual', '+'), ('Total', '')])
roc_df.columns = pd.MultiIndex.from_tuples([
('Predicted', '-'), ('Predicted', '+'), ('Total', '')])
roc_df.style.set_properties(**{'text-align': 'right'})
roc_df
[26]:
| Predicted | Total | |||
|---|---|---|---|---|
| - | + | |||
| Actual | - | 511 | 454 | 962 |
| + | 144 | 491 | 638 | |
| Total | 655 | 945 | 1600 | |
ROC curve plot¶
[27]:
dr_roc_green = '#03c75f'
white = '#ffffff'
dr_purple = '#65147D'
dr_dense_green = '#018f4f'
fig = plt.figure(figsize=(8, 8))
axes = fig.add_subplot(1, 1, 1, facecolor=dr_dark_blue)
plt.scatter(df.false_positive_rate, df.true_positive_rate, color=dr_roc_green)
plt.plot(df.false_positive_rate, df.true_positive_rate, color=dr_roc_green)
plt.plot([0, 1], [0, 1], color=white, alpha=0.25)
plt.title('ROC curve')
plt.xlabel('False Positive Rate (Fallout)')
plt.xlim([0, 1])
plt.ylabel('True Positive Rate (Sensitivity)')
plt.ylim([0, 1])
[27]:
(0, 1)
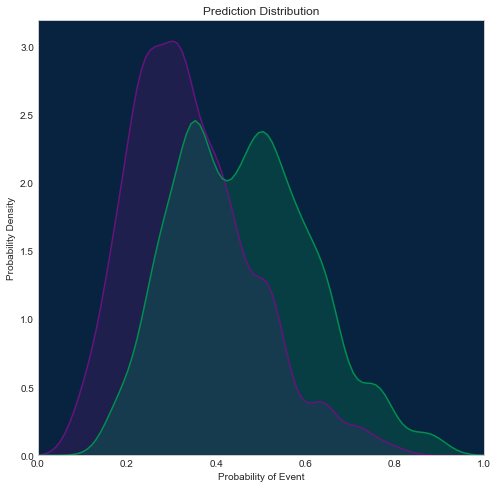
Prediction distribution plot¶
There are a few different methods for visualizing it, which one to use depends on what packages you have installed. Below you will find 3 different examples.
Using seaborn
[28]:
import seaborn as sns
sns.set_style("whitegrid", {'axes.grid': False})
fig = plt.figure(figsize=(8, 8))
axes = fig.add_subplot(1, 1, 1, facecolor=dr_dark_blue)
shared_params = {'shade': True, 'clip': (0, 1), 'bw': 0.2}
sns.kdeplot(np.array(roc.negative_class_predictions),
color=dr_purple, **shared_params)
sns.kdeplot(np.array(roc.positive_class_predictions),
color=dr_dense_green, **shared_params)
plt.title('Prediction Distribution')
plt.xlabel('Probability of Event')
plt.xlim([0, 1])
plt.ylabel('Probability Density')
[28]:
Text(0,0.5,'Probability Density')
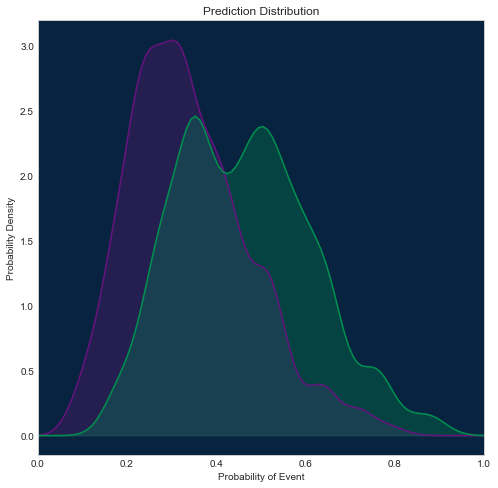
Using SciPy
[29]:
from scipy.stats import gaussian_kde
fig = plt.figure(figsize=(8, 8))
axes = fig.add_subplot(1, 1, 1, facecolor=dr_dark_blue)
xs = np.linspace(0, 1, 100)
density_neg = gaussian_kde(roc.negative_class_predictions, bw_method=0.2)
plt.plot(xs, density_neg(xs), color=dr_purple)
plt.fill_between(xs, 0, density_neg(xs), color=dr_purple, alpha=0.3)
density_pos = gaussian_kde(roc.positive_class_predictions, bw_method=0.2)
plt.plot(xs, density_pos(xs), color=dr_dense_green)
plt.fill_between(xs, 0, density_pos(xs), color=dr_dense_green, alpha=0.3)
plt.title('Prediction Distribution')
plt.xlabel('Probability of Event')
plt.xlim([0, 1])
plt.ylabel('Probability Density')
[29]:
Text(0,0.5,'Probability Density')
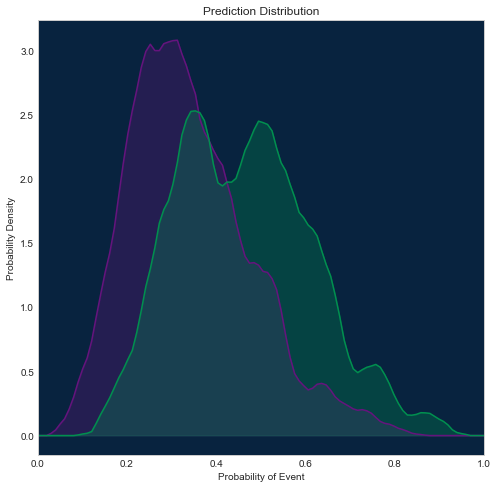
Using scikit-learn
This way will be most consistent with how we display this plot in DataRobot, because scikit-learn supports additional kernel options, and we can configure the same kernel as we use in web application (epanichkov kernel with size 0.05).
Other examples above use a gaussian kernel, so they may slightly differ from the plot in the DataRobot interface.
[30]:
from sklearn.neighbors import KernelDensity
fig = plt.figure(figsize=(8, 8))
axes = fig.add_subplot(1, 1, 1, facecolor=dr_dark_blue)
xs = np.linspace(0, 1, 100)
X_neg = np.asarray(roc.negative_class_predictions)[:, np.newaxis]
density_neg = KernelDensity(bandwidth=0.05, kernel='epanechnikov').fit(X_neg)
plt.plot(xs, np.exp(density_neg.score_samples(xs[:, np.newaxis])),
color=dr_purple)
plt.fill_between(xs, 0, np.exp(density_neg.score_samples(xs[:, np.newaxis])),
color=dr_purple, alpha=0.3)
X_pos = np.asarray(roc.positive_class_predictions)[:, np.newaxis]
density_pos = KernelDensity(bandwidth=0.05, kernel='epanechnikov').fit(X_pos)
plt.plot(xs, np.exp(density_pos.score_samples(xs[:, np.newaxis])),
color=dr_dense_green)
plt.fill_between(xs, 0, np.exp(density_pos.score_samples(xs[:, np.newaxis])),
color=dr_dense_green, alpha=0.3)
plt.title('Prediction Distribution')
plt.xlabel('Probability of Event')
plt.xlim([0, 1])
plt.ylabel('Probability Density')
[30]:
Text(0,0.5,'Probability Density')
Word Cloud¶
Word cloud is a type of insight available for some text-processing models for datasets containing text columns. You can get information about how the appearance of each ngram (word or sequence of words) in the text field affects the predicted target value.
This example will show you how to obtain word cloud data and visualize it in similar to DataRobot web application way.
The visualization example here uses colour and wordcloud packages, so if you don’t have them, you will need to install them.
First, we will create a color palette similar to what we use in DataRobot.
[31]:
from colour import Color
import wordcloud
[32]:
colors = [Color('#2458EB')]
colors.extend(list(Color('#2458EB').range_to(Color('#31E7FE'), 81))[1:])
colors.extend(list(Color('#31E7FE').range_to(Color('#8da0a2'), 21))[1:])
colors.extend(list(Color('#a18f8c').range_to(Color('#ffad9e'), 21))[1:])
colors.extend(list(Color('#ffad9e').range_to(Color('#d80909'), 81))[1:])
webcolors = [c.get_web() for c in colors]
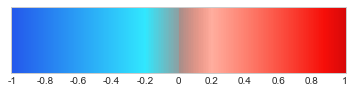
Variable webcolors now contains 201 ([-1, 1] interval with step 0.01) colors that will be used in the word cloud. Let’s look at our palette.
[33]:
from matplotlib.colors import LinearSegmentedColormap
dr_cmap = LinearSegmentedColormap.from_list('DataRobot',
webcolors,
N=len(colors))
x = np.arange(-1, 1.01, 0.01)
y = np.arange(0, 40, 1)
X = np.meshgrid(x, y)[0]
plt.xticks([0, 20, 40, 60, 80, 100, 120, 140, 160, 180, 200],
['-1', '-0.8', '-0.6', '-0.4', '-0.2', '0',
'0.2', '0.4', '0.6', '0.8', '1'])
plt.yticks([], [])
im = plt.imshow(X, interpolation='nearest', origin='lower', cmap=dr_cmap)
Now we will pick some model that provides a word cloud in the DataRobot. Any “Auto-Tuned Word N-Gram Text Modeler” should work.
[34]:
models = project.get_models()
[35]:
model_with_word_cloud = None
for model in models:
try:
model.get_word_cloud()
model_with_word_cloud = model
break
except ClientError as e:
if e.json['message'] and 'No word cloud data' in e.json['message']:
pass
else:
raise
model_with_word_cloud
[35]:
Model(u'Auto-Tuned Word N-Gram Text Modeler using token occurrences - diag_1_desc')
[36]:
wc = model_with_word_cloud.get_word_cloud(exclude_stop_words=True)
[37]:
def word_cloud_plot(wc, font_path=None):
# Stopwords usually dominate any word cloud, so we will filter them out
dict_freq = {wc_word['ngram']: wc_word['frequency']
for wc_word in wc.ngrams
if not wc_word['is_stopword']}
dict_coef = {wc_word['ngram']: wc_word['coefficient']
for wc_word in wc.ngrams}
def color_func(*args, **kwargs):
word = args[0]
palette_index = int(round(dict_coef[word] * 100)) + 100
r, g, b = colors[palette_index].get_rgb()
return 'rgb({:.0f}, {:.0f}, {:.0f})'.format(int(r * 255),
int(g * 255),
int(b * 255))
wc_image = wordcloud.WordCloud(stopwords=set(),
width=1024, height=1024,
relative_scaling=0.5,
prefer_horizontal=1,
color_func=color_func,
background_color=(0, 10, 29),
font_path=font_path).fit_words(dict_freq)
plt.imshow(wc_image, interpolation='bilinear')
plt.axis('off')
[38]:
word_cloud_plot(wc)
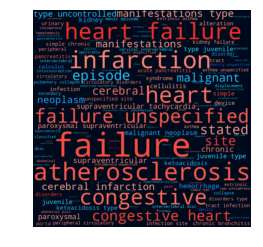
You can use the word cloud to get information about most frequent and most important (highest absolute coefficient value) ngrams in your text.
[39]:
wc.most_frequent(5)
[39]:
[{'coefficient': 0.6229774184805059,
'count': 534,
'frequency': 0.21876280213027446,
'is_stopword': False,
'ngram': u'failure'},
{'coefficient': 0.5680375262833832,
'count': 524,
'frequency': 0.21466612044244163,
'is_stopword': False,
'ngram': u'atherosclerosis'},
{'coefficient': 0.37932405511744804,
'count': 505,
'frequency': 0.2068824252355592,
'is_stopword': False,
'ngram': u'infarction'},
{'coefficient': 0.4689734305695615,
'count': 453,
'frequency': 0.18557968045882836,
'is_stopword': False,
'ngram': u'heart'},
{'coefficient': 0.7444542252245913,
'count': 452,
'frequency': 0.18517001229004507,
'is_stopword': False,
'ngram': u'heart failure'}]
[40]:
wc.most_important(5)
[40]:
[{'coefficient': -0.875917913896919,
'count': 38,
'frequency': 0.015567390413764851,
'is_stopword': False,
'ngram': u'obesity unspecified'},
{'coefficient': -0.8655105382141891,
'count': 38,
'frequency': 0.015567390413764851,
'is_stopword': False,
'ngram': u'obesity'},
{'coefficient': 0.8329465952065771,
'count': 9,
'frequency': 0.0036870135190495697,
'is_stopword': False,
'ngram': u'nephroptosis'},
{'coefficient': 0.7444542252245913,
'count': 452,
'frequency': 0.18517001229004507,
'is_stopword': False,
'ngram': u'heart failure'},
{'coefficient': 0.7029270716899754,
'count': 76,
'frequency': 0.031134780827529702,
'is_stopword': False,
'ngram': u'disorders'}]
Non-ASCII Texts
Word cloud has full Unicode support but if you want to visualize it using the recipe from this notebook - you should use the font_path parameter that leads to font supporting symbols used in your text. For example for Japanese text in the model below you should use one of the CJK fonts. If you do not have a compatible font, you can download an open-source font like this one from Google’s Noto project.
[41]:
jp_project = dr.Project.create('jp_10k.csv', project_name='Japanese 10K')
print('Project ID: {}'.format(project.id))
Project ID: 5c0008e06523cd0233c49fe4
[42]:
jp_project.set_target('readmitted_再入院', mode=AUTOPILOT_MODE.QUICK)
jp_project.wait_for_autopilot()
In progress: 2, queued: 12 (waited: 0s)
In progress: 2, queued: 12 (waited: 1s)
In progress: 2, queued: 12 (waited: 1s)
In progress: 2, queued: 12 (waited: 2s)
In progress: 2, queued: 12 (waited: 4s)
In progress: 2, queued: 12 (waited: 6s)
In progress: 2, queued: 11 (waited: 9s)
In progress: 1, queued: 11 (waited: 16s)
In progress: 2, queued: 9 (waited: 30s)
In progress: 2, queued: 7 (waited: 50s)
In progress: 2, queued: 5 (waited: 70s)
In progress: 2, queued: 3 (waited: 91s)
In progress: 2, queued: 1 (waited: 111s)
In progress: 1, queued: 0 (waited: 132s)
In progress: 2, queued: 5 (waited: 152s)
In progress: 2, queued: 3 (waited: 172s)
In progress: 2, queued: 2 (waited: 193s)
In progress: 2, queued: 1 (waited: 213s)
In progress: 1, queued: 0 (waited: 234s)
In progress: 2, queued: 14 (waited: 254s)
In progress: 2, queued: 14 (waited: 274s)
In progress: 2, queued: 12 (waited: 295s)
In progress: 1, queued: 12 (waited: 316s)
In progress: 2, queued: 10 (waited: 336s)
In progress: 2, queued: 9 (waited: 356s)
In progress: 2, queued: 7 (waited: 377s)
In progress: 2, queued: 6 (waited: 397s)
In progress: 2, queued: 4 (waited: 418s)
In progress: 2, queued: 3 (waited: 438s)
In progress: 2, queued: 1 (waited: 459s)
In progress: 1, queued: 0 (waited: 479s)
In progress: 1, queued: 0 (waited: 499s)
In progress: 0, queued: 0 (waited: 520s)
In progress: 2, queued: 3 (waited: 540s)
In progress: 2, queued: 1 (waited: 560s)
In progress: 1, queued: 0 (waited: 581s)
In progress: 1, queued: 0 (waited: 601s)
In progress: 2, queued: 2 (waited: 621s)
In progress: 2, queued: 0 (waited: 642s)
In progress: 0, queued: 0 (waited: 662s)
In progress: 1, queued: 0 (waited: 682s)
In progress: 0, queued: 0 (waited: 703s)
In progress: 0, queued: 0 (waited: 723s)
[43]:
jp_models = jp_project.get_models()
jp_model_with_word_cloud = None
for model in jp_models:
try:
model.get_word_cloud()
jp_model_with_word_cloud = model
break
except ClientError as e:
if e.json['message'] and 'No word cloud data' in e.json['message']:
pass
else:
raise
jp_model_with_word_cloud
[43]:
Model(u'Auto-Tuned Word N-Gram Text Modeler using token occurrences and tfidf - diag_1_desc_\u8a3a\u65ad1\u8aac\u660e')
[44]:
jp_wc = jp_model_with_word_cloud.get_word_cloud(exclude_stop_words=True)
[45]:
word_cloud_plot(jp_wc, font_path='NotoSansCJKjp-Regular.otf')

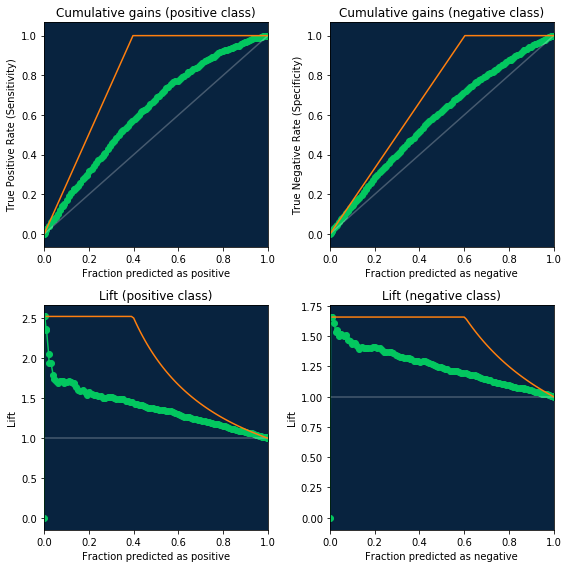
Cumulative gains and lift
ROC curve data also now contains information necessary for creating the cumulative gains and lift charts. Just use new fields fraction_predicted_as_positive and fraction_predicted_as_negative to get X axis and
- For cumulative gains use
true_positive_rate/true_negative_rateas Y axis - For lift use new fields
lift_positive/lift_negativeas Y axis.
You can check code for visualization below, along with baseline/random model (in gray) and ideal (in orange)
[46]:
fig, ((ax_gains_pos, ax_gains_neg), (ax_lift_pos, ax_lift_neg)) = plt.subplots(
nrows=2, ncols=2, figsize=(8, 8))
total_rows = (df.true_positive_score[0] +
df.false_negative_score[0] +
df.true_negative_score[0] +
df.false_positive_score[0])
fraction_of_positives = float(df.true_positive_score[0] +
df.false_negative_score[0]) / total_rows
fraction_of_negatives = 1 - fraction_of_positives
# Cumulative gains (positive class)
ax_gains_pos.set_facecolor(dr_dark_blue)
ax_gains_pos.scatter(df.fraction_predicted_as_positive, df.true_positive_rate,
color=dr_roc_green)
ax_gains_pos.plot(df.fraction_predicted_as_positive, df.true_positive_rate,
color=dr_roc_green)
ax_gains_pos.plot([0, 1], [0, 1], color=white, alpha=0.25)
ax_gains_pos.plot([0, fraction_of_positives, 1], [0, 1, 1], color=dr_orange)
ax_gains_pos.set_title('Cumulative gains (positive class)')
ax_gains_pos.set_xlabel('Fraction predicted as positive')
ax_gains_pos.set_xlim([0, 1])
ax_gains_pos.set_ylabel('True Positive Rate (Sensitivity)')
# Cumulative gains (negative class)
ax_gains_neg.set_facecolor(dr_dark_blue)
ax_gains_neg.scatter(df.fraction_predicted_as_negative, df.true_negative_rate,
color=dr_roc_green)
ax_gains_neg.plot(df.fraction_predicted_as_negative, df.true_negative_rate,
color=dr_roc_green)
ax_gains_neg.plot([0, 1], [0, 1], color=white, alpha=0.25)
ax_gains_neg.plot([0, fraction_of_negatives, 1], [0, 1, 1], color=dr_orange)
ax_gains_neg.set_title('Cumulative gains (negative class)')
ax_gains_neg.set_xlabel('Fraction predicted as negative')
ax_gains_neg.set_xlim([0, 1])
ax_gains_neg.set_ylabel('True Negative Rate (Specificity)')
# Lift (positive class)
ax_lift_pos.set_facecolor(dr_dark_blue)
ax_lift_pos.scatter(df.fraction_predicted_as_positive, df.lift_positive,
color=dr_roc_green)
ax_lift_pos.plot(df.fraction_predicted_as_positive, df.lift_positive,
color=dr_roc_green)
ax_lift_pos.plot([0, 1], [1, 1], color=white, alpha=0.25)
ax_lift_pos.set_title('Lift (positive class)')
ax_lift_pos.set_xlabel('Fraction predicted as positive')
ax_lift_pos.set_xlim([0, 1])
ax_lift_pos.set_ylabel('Lift')
ideal_lift_pos_x = np.arange(0.01, 1.01, 0.01)
ideal_lift_pos_y = np.minimum(1 / fraction_of_positives, 1 / ideal_lift_pos_x)
ax_lift_pos.plot(ideal_lift_pos_x, ideal_lift_pos_y, color=dr_orange)
# Lift (negative class)
ax_lift_neg.set_facecolor(dr_dark_blue)
ax_lift_neg.scatter(df.fraction_predicted_as_negative, df.lift_negative,
color=dr_roc_green)
ax_lift_neg.plot(df.fraction_predicted_as_negative, df.lift_negative,
color=dr_roc_green)
ax_lift_neg.plot([0, 1], [1, 1], color=white, alpha=0.25)
# ax_lift_neg.plot([0, fraction_of_positives, 1], [0, 1, 1], color=dr_orange)
ax_lift_neg.set_title('Lift (negative class)')
ax_lift_neg.set_xlabel('Fraction predicted as negative')
ax_lift_neg.set_xlim([0, 1])
ax_lift_neg.set_ylabel('Lift')
ideal_lift_neg_x = np.arange(0.01, 1.01, 0.01)
ideal_lift_neg_y = np.minimum(1 / fraction_of_negatives, 1 / ideal_lift_neg_x)
ax_lift_neg.plot(ideal_lift_neg_x, ideal_lift_neg_y, color=dr_orange)
# Adjust spacing for notebook
plt.tight_layout()
[ ]: